Draw a Box Form Intersections
In previous lessons, we used Venn diagrams to represent relationships between sets. Let'south await at the relationship of the sets described in instance one below.
Case 1:PermitX = {1, two, 3} and LetY = {iii, 4, 5}. What elements practiceTen andY accept in common?
Analysis: Nosotros will describe a Venn diagram of two overlapping circles. Elements that are common to both sets volition be placed in the middle part, where the circles overlap.
Solution:
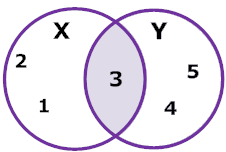
Explanation: The circumvolve on the left represents set upX and the circle on the right represents gear upY. The shaded region in the centre is what they have in common. That is their intersection. The intersection of setsX and Yis 3.
The Venn Diagram in example 1 makes information technology piece of cake to see that the number 3 is common to both sets. And then the intersection ofX andY is 3, and this is written every bit:
X ∩ Y = {3}
| Definition: | The intersection of 2 sets,X andY, is the fix of elements that are common to bothX andY. It is denoted past Ten ∩ Y, and is read "10 intersect Y". |
So the intersection of 2 sets is the set of elements common to both sets. Let'due south wait at some more examples of intersection.
Instance 2: Let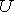 = {counting numbers},P = {multiples of 3 less than 20} andQ = {fifty-fifty numbers less than 20}. Draw and label a Venn diagram to show the intersection ofP andQ.
= {counting numbers},P = {multiples of 3 less than 20} andQ = {fifty-fifty numbers less than 20}. Draw and label a Venn diagram to show the intersection ofP andQ.
Analysis: Start by filling in the elements in the intersection. SinceP = {3, 6 , 9, 12 , 15, 18 } andQ = {2, 4, half dozen , 8, 10, 12 , fourteen, 16, 18 }, we know that half-dozen , 12 and 18 volition be filled in first.
Solution:
Notation: P ∩ Q = {6, 12, xviii}
Some other manner to define the intersection of two sets is as follows:
A ∩ B = { x | x 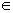 A and 10
A and 10 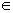 B }
B }
The procedure for drawing the intersection of two sets is shown beneath.
Procedure for Cartoon the Intersection of Ii Sets Overlapping Sets
Step one:
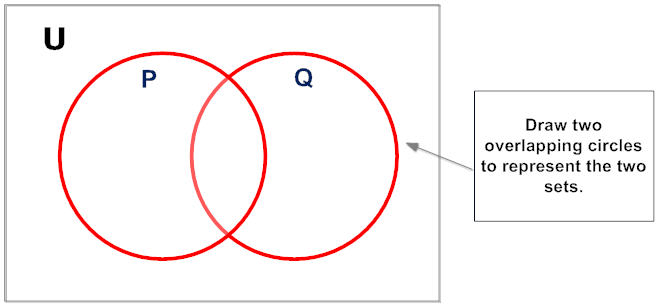
Step 2:
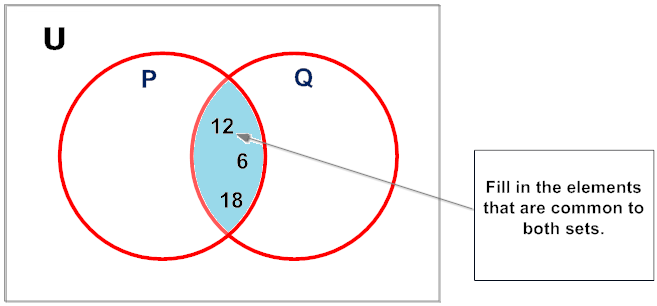
Step iii:
Permit'south look at the intersection of other types of sets. In example three below,the given sets are not overlapping.
Example three: Permit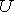 = {animals},A = {dogs} andB = {cats}. Draw and label a Venn diagram to show the intersection ofA andB.
= {animals},A = {dogs} andB = {cats}. Draw and label a Venn diagram to show the intersection ofA andB.
Analysis: SetsA andB do not overlap. These sets are disjoint, and take no elements in mutual.
Solution:
Note: A ∩ B = Ø
Two setsA andB are disjoint if their intersection is naught. This is denoted by A ∩ B = Ø ,whereØ is the null orempty set.
Recall thataUniversal Set is the set of all elements under consideration, denoted past capital . All other sets are subsets of the universal gear up. So in each instance in a higher place, the circles are subsets of the Universal fix. We have examined the intersection of overlapping sets, and of disjoint sets. Let's await at the intersection of one set up independent within another.
. All other sets are subsets of the universal gear up. So in each instance in a higher place, the circles are subsets of the Universal fix. We have examined the intersection of overlapping sets, and of disjoint sets. Let's await at the intersection of one set up independent within another.
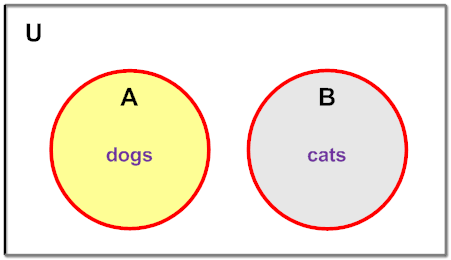
Case 4:Permit C = {a, r, eastward} and D = {f, a, i, r, e, s, t}. Depict and characterization a Venn diagram to show the intersection of sets C and D.
Assay: C is a subset of D. Recollect that this is denoted by C D.
Solution:
Explanation: It turns out that C ∩ D = {a, r, east}, which is equal to the set C.
In case 4, since C 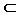 D , nosotros get that C∩ D = C . This relationship is defined below.
D , nosotros get that C∩ D = C . This relationship is defined below.

The process for drawing the intersection of i set contained within another is shown below.
| Procedure for Drawing the Intersection of 1 Set Contained Within Another | |
| Step 1: | Draw one circumvolve within another circumvolve. |
| Pace ii: | Write down the elements in the inner circle. |
| Step iii: | Write down the remaining elements in the outer circle. |
Let'south see if you tin can follow the challenge presented in Example 5.
Case v:Given the Venn diagram below, proper name a member of Band that is not in both Band and Chorus.
Analysis: This problem is request us to observe a member of Band that is not in the intersection of Ring and Chorus.
Solution:
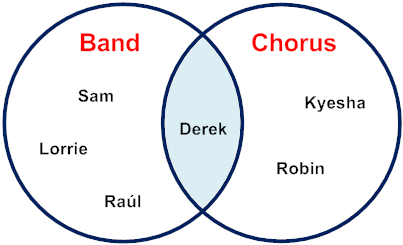
Explanation: Sam, Lorrie and Raúl are each members of Ring only. In improver, these students are not in Band and Chorus.
Summary:The intersection of two sets A and B, denoted by A ∩ B, is the prepare of elements that are common to both A and B. The formal definition of intersection is shown below.
A ∩B = {x |x 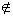 A and ten
A and ten 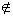 B}
B}
Exercises
Directions: Draw and label a Venn Diagram to help you lot answer each question beneath. Select your answer by clicking on the corresponding button. Feedback to your respond is provided in the RESULTS BOX. If you lot make a mistake, rethink your respond, then choose a dissimilar button.
| 4. | Given 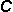 = {Saturday, Sunday} and = {Saturday, Sunday} and 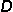 = {Mon, Tuesday, Wednesday, Thursday, Friday, Saturday, Dominicus}, what is = {Mon, Tuesday, Wednesday, Thursday, Friday, Saturday, Dominicus}, what is 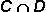 ? ? |
Sign Up For Our Gratuitous Newsletter!
Sign Upwardly For Our FREE Newsletter!
Source: https://www.mathgoodies.com/lessons/sets/intersection